
Click to learn more about author Thomas Frisendal.
Remember?
People of my age were taught set algebra at high-school (in my case in the late seventies). Today it is elementary school stuff. And it is indeed a useful tool with applications in many real-life situations.
Why did Set Algebra not Become More Popular?
In retrospect, set algebra never made it big time within it tools, applications and databases.
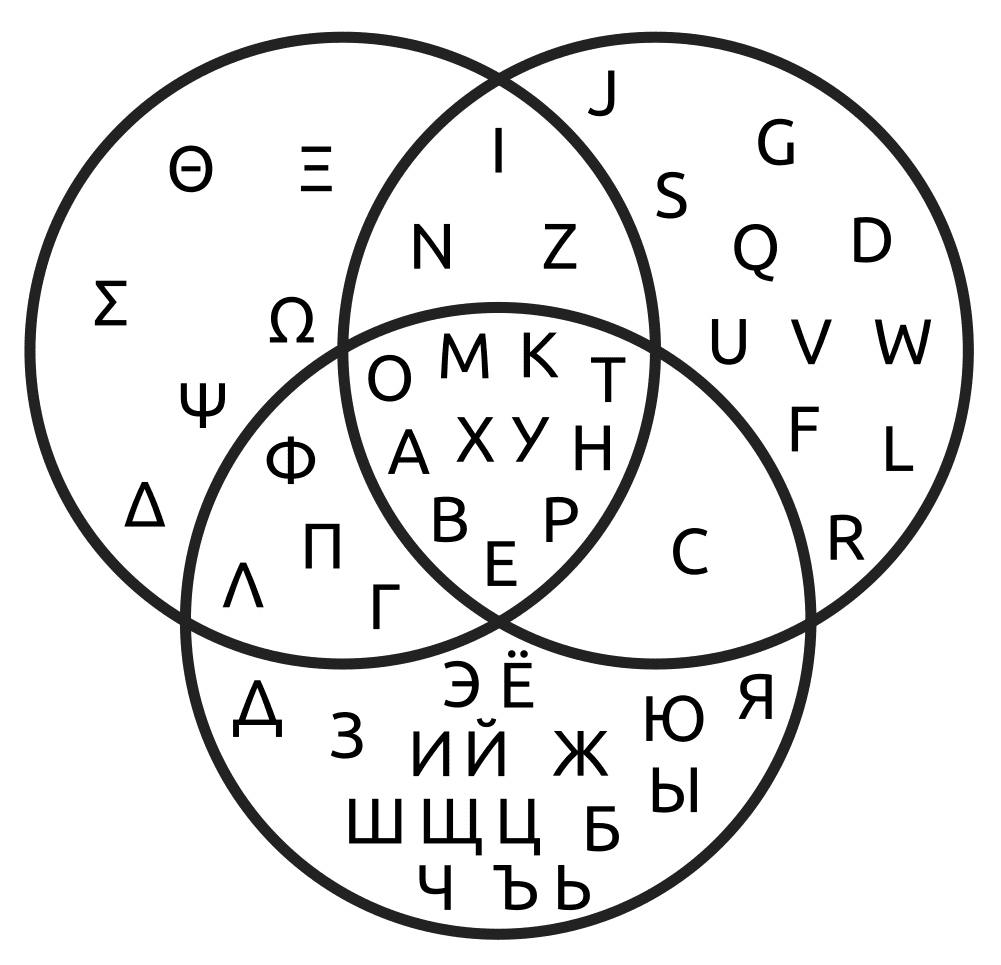
Venn diagram showing the uppercase glyphs shared by the Greek, Latin, and Cyrillic alphabets – From WikiMedia Commons (Watchduck (a.k.a. Tilman Piesk) [Public domain]
If fact, most of what has been exposed is the SQL set-style operators (UNION, INTERSECTION and DIFFERENCE), of which UNION made it into the first SQL standard in 1986, and the rest followed in SQL-92 (I believe).
The SQL operators were meant to implement the relational algebra as proposed by Dr. Ted Codd. Unfortunately Dr. Codd based some of his ideas on a ”extended set theory”, which was an idea formulated and described in a 1977 paper:
“Extended set theory” by D. L. Childs, VLDB ’77 Proceedings of the third international conference on Very large data bases – Volume 3, (https://dl.acm.org/citation.cfm?id=1286584).
But Childs’ extensions were not ideally suited, which is explained in quite some detail in this book: The Algebra of Data – A Foundation for the Data Economy by Professor Gary Sherman & Robin Bloor, Ph.D. © 2015 by The Bloor Group Press.
The (latter) authors argue that mainstream Zermelo-Fraenkel set theory (Cantor), would have been a better starting point. One key issue is that sets should be able to be sets of sets.
Nevertheless, what happened to set algebra after having been endorsed by the SQL standard?
Who are Actually Using Sets?
Set operations did not really break out of the SQL zone. I have been writing tons of SQL and in my experience, UNION is used sometimes, whereas INTERSECT and DIFFERENCE are not used very much (and mostly in metadata operations). UNION is most often used as ”the poor DBA’s ETL-tool to consolidate data having different shapes from different systems into one structure, often as part of a view (and often spraying NULL’s all over the place).
For many years I was hoping to see some set algebra in end-user oriented applications. The only product that I know of, and I have been on the lookout for almost 40 years, is a nice product called Set Analyzer, which came into existence in the 80s (?), and was bought by Business Objects a few years later. The use case was customer segmentation
The tool used Venn diagrams as part of the UI controls:
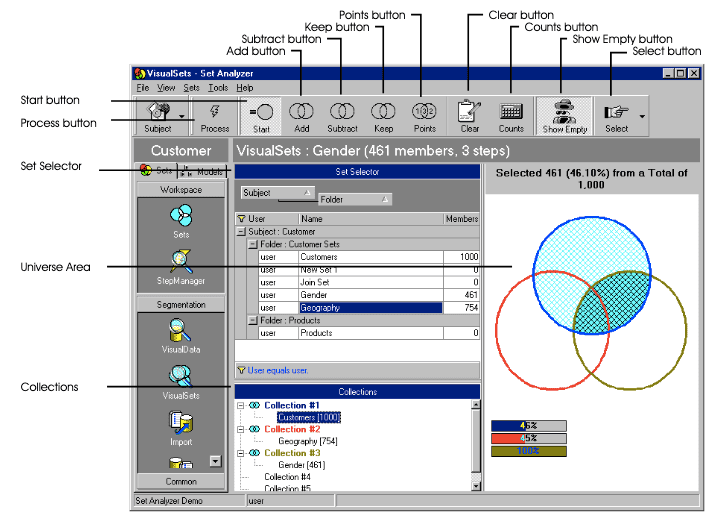
The functionality is apparently still alive and kicking (?) now that it belongs to SAP: (The company Business Objects was acquired by SAP).
Today the product is called ”SAP Business Objects Set Analysis”. There is a 2017, elaborate, YouTube video from SAP called Set Analysis in SAP Business Objects Web Intelligence, Using Information Design Tool.
In essence the product maintains lists of customers, who are interesting from a marketing perspective. To me it is interesting that these lists are built, combined, and maintained using the set algebra paradigm. But it is still a tabular solution.
The Business Cases
The most obvious use case was/is customer segmentation (customer behavior analysis) and product campaign planning in marketing applications.
Today there are also strong user stories in the contexts of investigative work flows based on sets of suspects in graph-based analysis of crime, intelligence, fraud, churn, recommendations and other behavior / networking analytical areas.
I really encourage you to read the Business Object fact sheet (ref. above).
The basic user story is:
- I (as a business user) can define “sets” as search results
- I can save sets with a name and recall them
- I can use set algebra (just like I learned at school), and also use conditions on sets in order to create new sets
- I use this to plan my campaigns across my different customer segments.
This enables sophisticated, iterative analytics on combinations of sets. Useful in marketing and CRM, which is what the product was designed for. Today social network analysis, fraud, law enforcement and much more promise even better payback than good CRM.
The current SAP version has the notion of “temporary” which means “as of now” (i.e. do the search again), or “static” meaning as of the last result of the search (which can be done again).
So, SAP still has a “killer application” in the area of end-user tools for set algebra. And an application is necessary, because writing complex SQL queries is a daunting task for most marketing analysts.
But today there are “NoSQL opportunities”…
Graphs are Sets
As you may know from well publicized projects like the Panama Papers etc. graphs offer a very rich context. It could well be that the SQL set operations never really gained traction, because most of the use cases require a rich context?
In my opinion sets of graphs is a once-in-a-lifetime opportunity that is much more than a revival: Doing set algebra on sets of graphs is potentially several orders of magnitude more powerful than SQL-based set algebra (or the simple lists etc. offered by early set analysis tools such as the BO Set Analyzer).
All sets are not graphs. But graphs are sets. In the Data Algebra book by Sherman and Bloor (cf. reference above) there is a good argumentation for this. In fact there is a whole chapter (7) called Data Algebra and Graphs. I am not going to repeat that chain of arguments, but basically graphs can be understood as a relationship (which is not Dr. Codd’s kind, and which in the data algebra parlance is called a “clan”), which in turn consists of “couplets” (e.g. representing a start node, the relationship and an end node). I refer you to the book for the mathematics about building the hierarchy going from data to couplets over clans to “hordes”. If the math holds, and I think it does (Algebraix Data has patented it?), graphs (being “clans” of couplets) can be subjected to:
- Union and cross-unions as well as
- Intersection and cross-intersections.
And sets of graphs have a lot more information than plain sets of the tabular kind. That is the real opportunity here.
In consequence I challenge the graph database vendors to prove that the set algebra support should happen by way of simple, intuitive declarations in an end-user friendly graph query language. (Tool vendors are most welcome to add some cool visuals).
A User Story
Let me describe the challenge as a user story.
As a marketing analyst I am trying to establish potential churners among the customers. I have some graphs established for various kinds of behavior:
- No purchases last 6 months
- VIP card owners
- Logins last 12 months
- High income residentials
So, I want to target some potential churners, whom I would hate to loose as customers. Thus creating a new set called “Hate to loose” comprising:
“In set A, but only members of set D, who are in set B and who are not in set C.”
In classic math notation, it is something like:
Hate to loose = No purchases last 6 months ∩
((High income residentials – Logins last 12months) ∪ VIP card owners)
Or something like that. What about a graph query like this:

The create graph statement above could be an extension of the Cypher query language, which is one of the leading query languages for property graph databases. Obviously it would be easy to add a nice Euler-/Venn diagram visualization on top, hiding the statement syntax for casual users.
However, in the graph space there are analytical people working on the graph structure level in a declarative language. Think fraud investigators as the business users and what they would like to be able to do.
Conclusion
There are not many additional things to do in order to provide a good platform for building solutions, which employ set algebra style applications on top of sets of graphs.
The business benefits of being able to do so are substantial. Who will get there first? SAP has an advantage. What about Neo4j? Both of them support Cypher. And there are other contenders. Stay tuned.
