
You thought you knew all normal forms?
(And possibly also some abnormal …)
Well, think again: There is also “graph normal form (GNF).”
The diagram below is a fifth normal form graph concept model, which is just a few steps from GNF, so hang on:
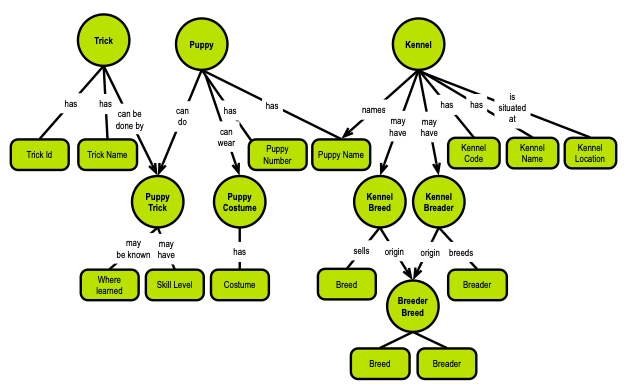
Where GNF comes from
GNF is based on serious mathematics, going back at least 25 years. At the end of this post, you will find some selected academic references, most of them related to formal logic. The mathematicians were looking for ways to build a canonical representation of graphs to be able to compare them. They found ways to do that, and many called it “graph normal form.” The above sentence is my simple, naïve explanation for non-mathematicians. If you are a trained logician, you could try to read Dyrkolbotn, 2012 (cf. below), for an explanation using formal logic.
Some of those academic papers are pointing backward to J. F. Sowa and his semantic networks (from the ’90s, aka known as conceptual graphs), and also pointing in the direction of the Common Logic language, which has been an ISO standard (24707) since 2007.
But there is also a commercial track in this. Aref et al (cf. below), when at LogicBlox in 2015, published a SIGMOD paper (cf. below) of their implementation of graph normal form. This has led to the company Relational AI (RAI, the successor of LogicBlox). Their take is that relational is fine, also for analytics, but only if you deconstruct the SQL model to a graph normal form model. In addition, you need to be very good at doing multi-way joins. On top of that, add machine generation of various aspects of functional dependencies, including key handling. At the end of this post you will find a link to RAI’s to-the-point explanation of their products’ capabilities.
Graph Normal Form Extends Relational Normalization
Why normal forms are necessary
GNF is based on the decompositions of relational normalization. Let us, therefore, begin with a quick recap of what one could call “orthodox normalization” by way of a famous example. (If you are an experienced relational normalizer, you may want to skip this section.)
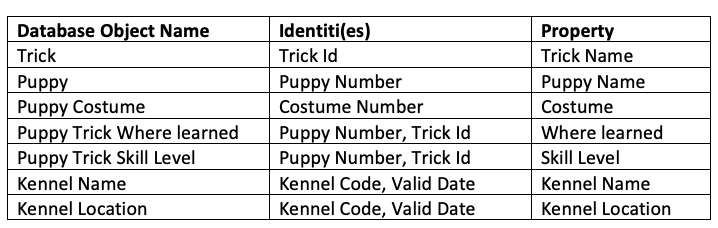
The example is in a kennel-puppy-tricks fictional context and it appeared as a complimentary poster in the Database Programming & Design Magazine published by Miller Freeman back in 1989. The intellectual rights belong to Marc Rettig, now of Fit Associates. It is included here with his kind permission, cf. the low-res image at the end this post (including a link to a high-res version).
The following explanations are loyal to the text on the poster but are compacted (by yours truly).
RULE 1: Eliminate Repeating Groups
Make a separate table for each set of related attributes and give each table a primary key.

In the original list of data, each puppy’s description is followed by a list of tricks the puppy has learned. Some might know 10 tricks, some might not know any. To answer the question, “Can Fifi roll over?” we need to first find Fifi’s puppy record, then scan the list of tricks at the end of that record. This is awkward, inefficient, and untidy.
Moving the tricks into a separate table helps considerably:

Separating the repeating groups of tricks from the puppy information results in first normal form. The puppy number in the trick table matches the primary key in the puppy table, providing the relationship between the two.
RULE 2: Eliminate Redundant Data
If an attribute depends on only a part of a multi-valued key, move it to a separate table.
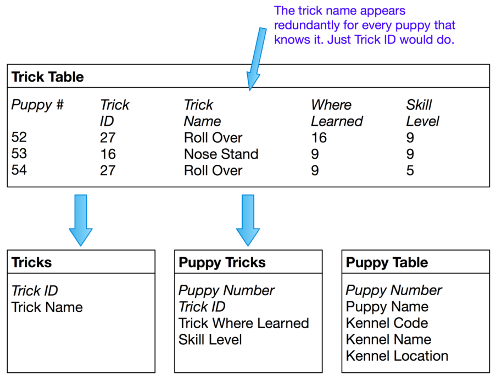
In the Trick Table in the first normal form, the primary key is made up of the puppy number and the trick ID. This makes sense for the “where learned” and “skill level” attributes, since they will be different for every puppy/trick combination. But the trick name depends only on the trick ID. The same name will appear redundantly every time its associated ID appears in the Trick Table.
Suppose you want to reclassify a trick – give it a different trick ID. The change needs to be made for every puppy that knows the trick! If you miss some, you’ll have several puppies with the same trick under different IDs. This represents an “update anomaly.”
Or suppose the last puppy knowing a particular trick gets eaten by a lion. His records will be removed from the database, and the trick will not be stored anywhere! This is a “delete anomaly.” To avoid these problems, we need the second normal form (as in the diagram above).
To achieve this, separate the attributes that depend on both parts of the key from those depending only on the trick ID. This results in two tables: “Tricks,” which gives the name for each trick ID, and “Puppy Tricks,” which lists the tricks learned by each puppy.
RULE 3: Eliminate Columns Not Dependent on Key
If attributes do not contribute to a description of the key, move them to a separate table.
The key of the Puppy Table is puppy number, but the kennel name and kennel location describe only a kennel (not a puppy). To achieve third normal form, they must be moved into a separate table. Since they describe kennels, kennel code becomes the key of the new “Kennels” table. The motivation for this is the same as for second normal form: we want to avoid update and delete anomalies. For example, suppose no puppies from the Daisy Hill Puppy Farm were currently stored in the database. With the previous design, there would be no record of Daisy Hill’s existence!
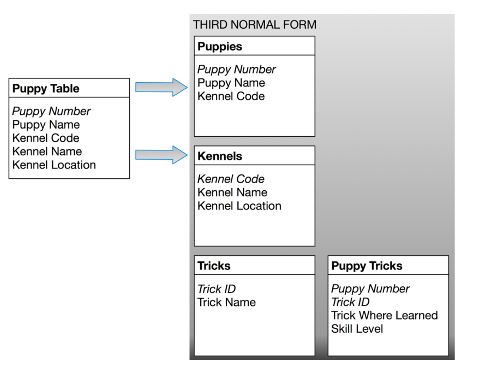
RULE 4: Isolate Independent Multiple Relationships
No table may contain two or more 1:n or n:m relationships that are not directly related.
Rule Four applies only to designs that include one-to-many and many-to-many relationships. An example of one-to-many is that one kennel can hold many puppies. An example of many-to-many is that a puppy can know many tricks, and many puppies might know the same trick.
Suppose we want to add a new attribute to the Puppy Trick table: “Costume.” This way we can look for puppies that can both “sit up and beg” and wear a Groucho Marx mask, for example. Fourth normal form dictates against using the Puppy Trick table because the two attributes do not share a meaningful relationship. A puppy may be able to walk upright, and it may be able to wear a suit. This doesn’t mean it can do both at the same time. How will you represent this if you store both attributes in the same table?
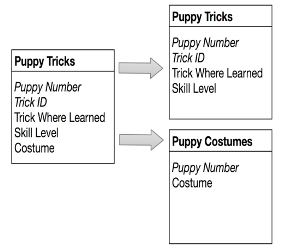
RULE 5: Isolate Semantically Related Multiple Relationships
There may be practical constraints on information that justify separating logically related many-to-many relationships.
Imagine that we now want to keep track of dog breeds and breeders. Our database will record which breeds are available in each kennel. And we want to record which breeder supplies dogs to those kennels. This suggests a Kennel-Breeder-Breed table that satisfies fourth normal form. As long as any kennel can supply any breed from any breeder, this works fine.
Now suppose a law is passed to prevent excessive arrangements: a kennel selling any breed must offer that breed from all breeders it deals with. In other words, if Kabul Kennels sells Afghans and wants to sell any Daisy Hill puppies, it must sell Daisy Hill Afghans.
The need for a fifth normal form becomes clear when we consider inserts and deletes. Suppose a kennel decides to offer three new breeds: Spaniels, Dachshunds, and West Indian Banana-Biters. Suppose further that it already deals with three breeders that can supply those breeds. This will require nine new rows in the Kennel-Breeder-Breed table – one for each breeder/breed combination.
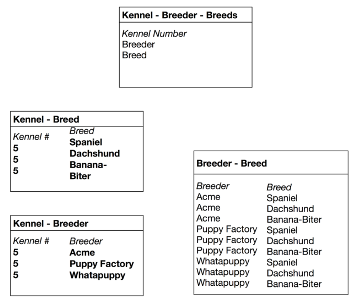
Breaking up the table reduces the number of inserts to six. Above are the tables necessary for fifth normal form, shown with the six newly inserted rows in bold type. If an application involves significant update activity, fifth normal form can save important resources.
This is the end of the text from the original poster.
Visualizing the Structure of the Data Using Graphs
Why graphs are representations of functional dependencies
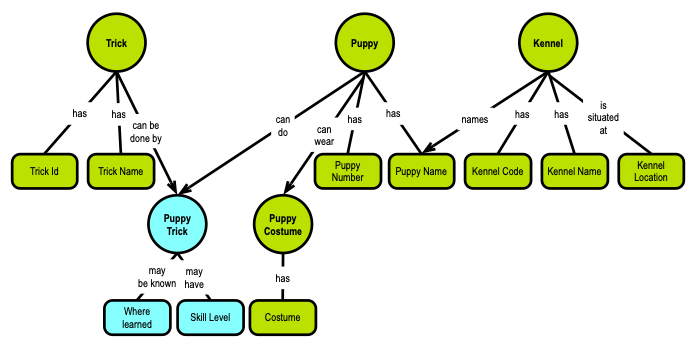
Actually, the little graph at the beginning of this post shows the very same table structure, which the poster developed (as described above):

So, the concept model above represents a fifth normal form (5NF) of the Puppies data model. There are two kinds of concepts: things (the round ones) and attributes/properties (the rounded rectangles). And the semantics is explicit via the named relationships with cardinalities. The semantics reflect the functional dependencies, as they are called in the relational model.
Take-away: Relationships in graphs represent functional dependencies with cardinalities.
So, are there any additional structural things that we need?
Yes: identity and uniqueness. These two qualities contribute hugely to setting the context in precise ways. The rationale for relational normalization was not clearly stated from a business perspective, but the benefits are clearly related to identity and uniqueness.
Humans do not really care about uniqueness. What is in a name, anyway? We all know that “James Brown” can refer to a very large number of individuals. The trick is to add context: “Yes, you know, James Brown, the singer and the Godfather of Soul.” When uniqueness really matters, context is the definite answer.
The requirement for unique identification is, then, an IT-derived necessity. This gave rise to the “artificial” identifiers (Social Security Number, for example) on the business level and the system-generated “ID” fields (aka surrogate keys) on the database level. We, as data modelers, must handle these difficult issues in a consistent manner across:
- Identity
- Uniqueness
- Context.
And this realm is governed by the functional dependencies.
Functional Dependencies Revisited
Why functional dependencies rule
The end result of the discussion is that identity is functionally derived from uniqueness, which sets the context. This is the foundation of the commonly discussed “functional dependencies” in relational modeling, including the whole of normalization, candidate keys, primary and foreign keys and runtime query predicates, etc. If you are interested in going deeper into this, you can see very detailed explanations of the handling of functional dependencies in 16 different parts of SQL query resolutions ISO/IEC 9075-2:2016, Information technology – Database languages – SQL – Part 2: Foundation (SQL/Foundation – licensed document). It is important to understand that SQL implementations must be capable of inferring the various functional dependency situations at runtime.
In a graph context this becomes simpler:
Skill level shares scope with where learned, and both are driven by the identity of the puppy trick. For now, we need to establish a reliable identity of puppy trick. This used to be referred to as “establishing the primary key.”
Uniqueness is the matter of identifying what (on the business level) makes an identity unique. If you are a data modeler, you will not be surprised by the uniqueness behind puppy trick:
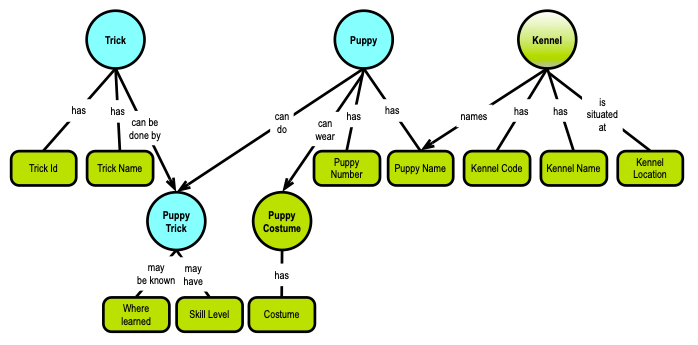
Yes, the puppy trick is uniquely defined by the combination of trick and puppy (i.e., whatever their identities are defined as). Previously this was called “foreign keys,” but remember that foreign keys in SQL are not mandatory and are frequently not being implemented for performance reasons. So, even the basic dependencies such as foreign keys may not be explicit, but can be inferred from the where clauses, for instance, at runtime.
I always take care to have two levels of identities and uniqueness:
- Business level keys for identities and concatenation of business keys for uniqueness
- Physical level unique keys (possibly generated UUIDs or other surrogate keys) – mapping from business keys to physical keys.
Frequently there are needs for machine generation of business level keys, where none exists already, as well as plenty of physical level keys.
Hidden dependencies – Paving the Way for Sixth Normal Form
Why including other (not explicit) dependencies is necessary
Implicit foreign keys is only one example of hidden dependencies.
Nulls can be explicitly specified, but you may want to not have them, at all. There is a solution for that, which in relational modeling is known as sixth normal form.
In our little Puppies example, not many attributes seem to be nullable. Maybe the Location of a Kennel is not always known. This means that the Kennel table should be decomposed into its individual components, Location being on of them; so we define a Kennel-Location table. If the Location is not known, there is simply no row for it the the new Kennel-Location table.
Another common data model phenomenon is the issue of categories. You may choose to treat them as passive data, or you may choose to give them full “data base object rights,” including their own identity and possibly temporal variations. There are no examples of this in the Puppies example.
Finally, temporal variations is pushing hard for going to sixth normal form. In some use cases, the updating frequencies for individual properties of things (objects) are not bundled. Take the Kennel Location, for example: A Kennel may well change locations over time, but it is still the same Kennel. This implies that many properties follow their own timelines (which may be shared by a set of properties across the data model). If the requirement is to keep time-stamped versions of data, sixth normal form is the way to go.
Both fifth and sixth normal forms are frequently used in data warehousing modeling approaches such as data vault and anchor modeling.
Graph Normal Form – GNF and 6NF
Why sixth normal form matter and graph normal form are essentially the same
Let us, then, move our Puppies to Graph Normal Form. To begin with, I have made a couple of extensions to the fifth normal form of the Puppies data model:
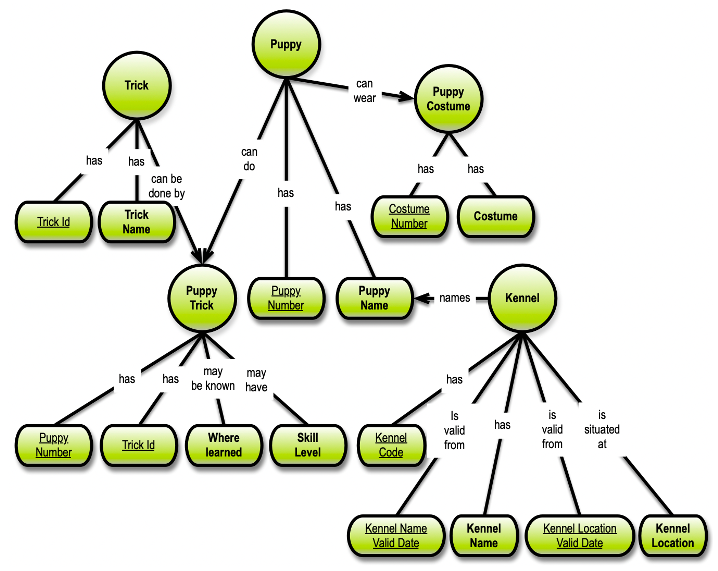
I have left out the Breed/Breeder parts of the original example, but I have added two “valid dates” to get two temporal aspects of Kennel. I also added Costume Number to the model. Note that Where learned is not mandatory (“may …”), so even in this simple model, we have temporal and nullability reasons for going to sixth normal form.
I also underlined the identities; they are driving the physical structure of the 6NF data model, if that is what you want:
Overall, there are two major steps in going from 5NF to GNF:
- Make sure that you have (business-level) identities on everything – no single attribute concept should be independent of identities, and
- Make sure that you have (business-level) uniqueness of every 6NF object that you are going to create.
Visualization of Graph Normal Form
Finally, here we have a visualization of graph normal form (GNF), which also helps understanding the underlying 5NF and its’ dependencies:

The white circles are not physical 6NF database objects; only logical Concepts serving as visual aids for understanding the graph structure.
In a physical graph database, I would carry over the semantics as the relationships, just like in the 5NF concept model. In a SQL representation of the same thing, I could reflect the relationship names in the physical table names (e.g., “PuppyCanWearCostume,” “KennelHasKennelName,” and “KennelIsSituatedAtKennelLocation,” etc).
Caveat: Only the brave-hearted implement physical foreign keys for all relationships in a 6NF database, and do 25+ way joins in an off-the-shelf SQL DBMS. You need a graph database (or other NoSQL solutions), and/or you could talk to Relational AI (see link below).
Key point: GNF is the “atomic” (canonical) representation of any data model. This means that you can reduce data models to GNF (by way of machine generation), and you can also aggregate GNF to e.g. property graphs, SQL, JSON, and what have you. GNF is also the place to go for modeling immutable, versioned, journaled (parts of) ledger databases (not to say blockchain).
My take:
Graph Normal Form, GNF, feels a lot like the planet, where all data models can all live happily together!
Resources
Relational AI has, as the first software company that I know of, based their strategy on graph normal form and they also offer 6NF multiway join support. See this fine, and short, explanation of GNF (including video).
The Puppies example appeared as a complimentary poster in the Database Programming & Design Magazine published by Miller Freeman back in 1989. The intellectual rights belong to Marc Rettig, now of Fit Associates. It is included here with his kind permission:

The concept mapping diagrams in my text is from my 2016 book on Graph Data Modeling.
Selected academic references with relevance to graph normal form:
Abdi, S. and Gajski, D., “Functional validation of system level static scheduling,” Design, Automation and Test in Europe, 2005, pp. 542-547 Vol. I
Aref, M., et al, Design and Implementation of the LogicBlox System, Proceedings of the 2015 ACM SIGMOD International Conference on Management of Data
Bezem, M., Grabmayer, C., and Walicki, M., Expressive power of digraph solvability. Annals of Pure and Applied Logic, vol. 163 (2012), no. 3, pp. 200–212.
Cook, B., Haase, C., Ouaknine, J., Parkinson, M., Worrell, J., Tractable Reasoning in a Fragment of Separation Logic. In: Katoen, JP., König, B. (eds) CONCUR 2011 – Concurrency Theory. CONCUR 2011. Lecture Notes in Computer Science, vol 6901. Springer
Cook, R., Patterns of paradox, this Journal, vol. 69 (2004), no. 3, pp. 767–774.
Dyrkolbotn, S. and Walicki, M., Propositional discourse logic. Synthese, vol. 191 (2014), no. 5, pp. 863–899.
Dyrkolbotn, S., “Doing argumentation using theories in graph normal form.” ESSLLI. 2012.
Green, T. J., Huang, S., Loo, B.T., Zhou, W., Datalog and Recursive Query Processing, Foundations and Trends R© in Databases, Vol. 5, No. 2 (2012) pp. 105–195.
Simonet, G., Two FOL semantics for simple and nested conceptual graphs. In: Mugnier, ML., Chein, M. (eds) Conceptual Structures: Theory, Tools and Applications. ICCS 1998. Lecture Notes in Computer Science, vol 1453. Springer
Walicki, M., Resolving infinitary paradoxes. The Journal of Symbolic Logic, 82(2), 709-723.